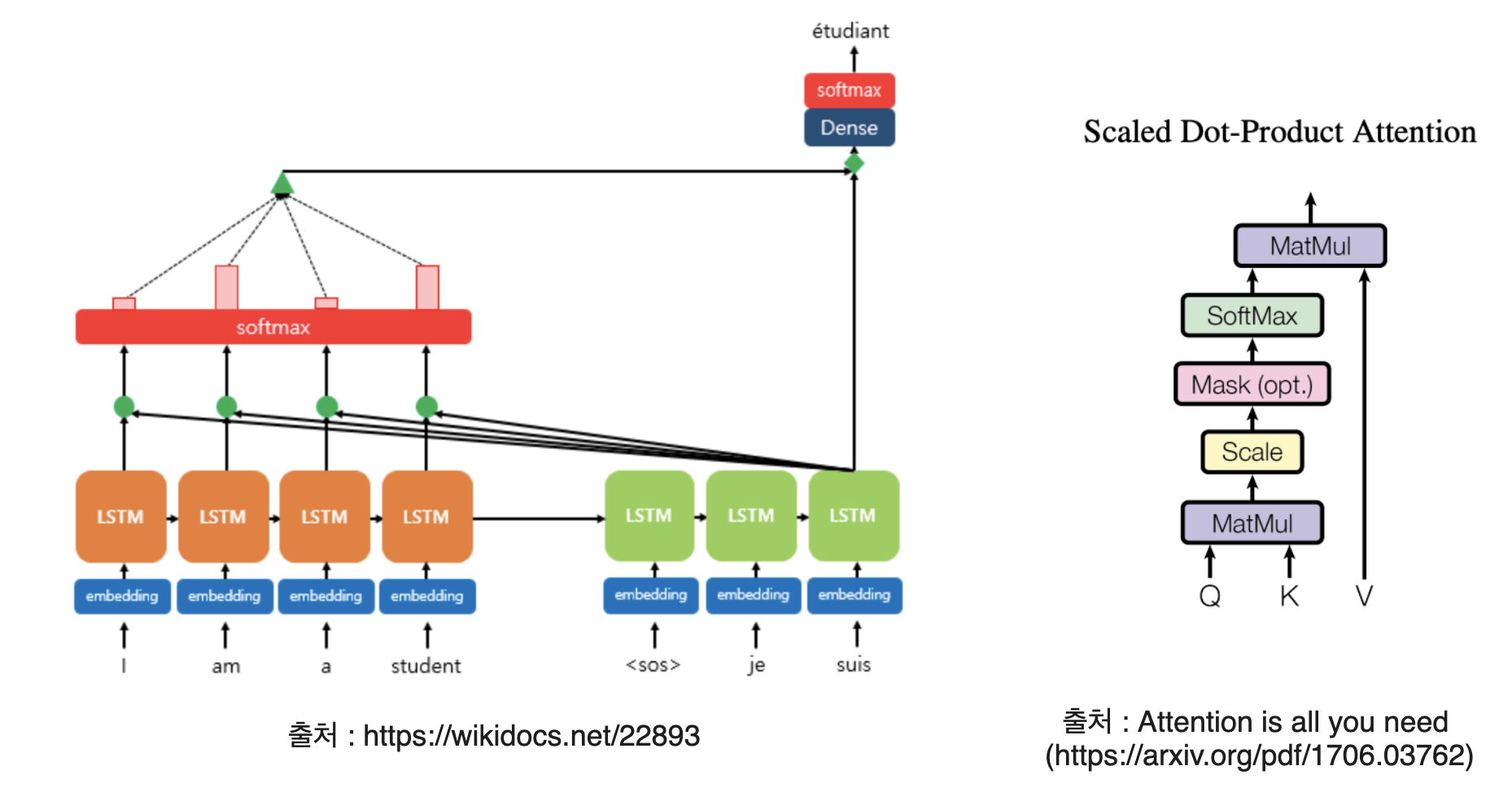
좌측의 사진을 보면, 이전 글에서 설명한 Sequence-to-sequence와 같은 구조를 가지고 가는 것을 알 수 있다. 하지만, RNN(또는 LSTM)을 사용하게 되면 발생하는 Vanishing Gradient Problem이 발생할 수 밖에 없다. 만약, Encoder의 첫 Input이 영향을 크게 줘야한다면 영향을 주기 어렵다는 뜻이 된다. 이를 해결하기 위해, 좌측의 사진처럼 Encoder Section의 값을 모두 검토하는 방식을 채택하게 된다.
단계별 분석
Step1. Attention score 구하기
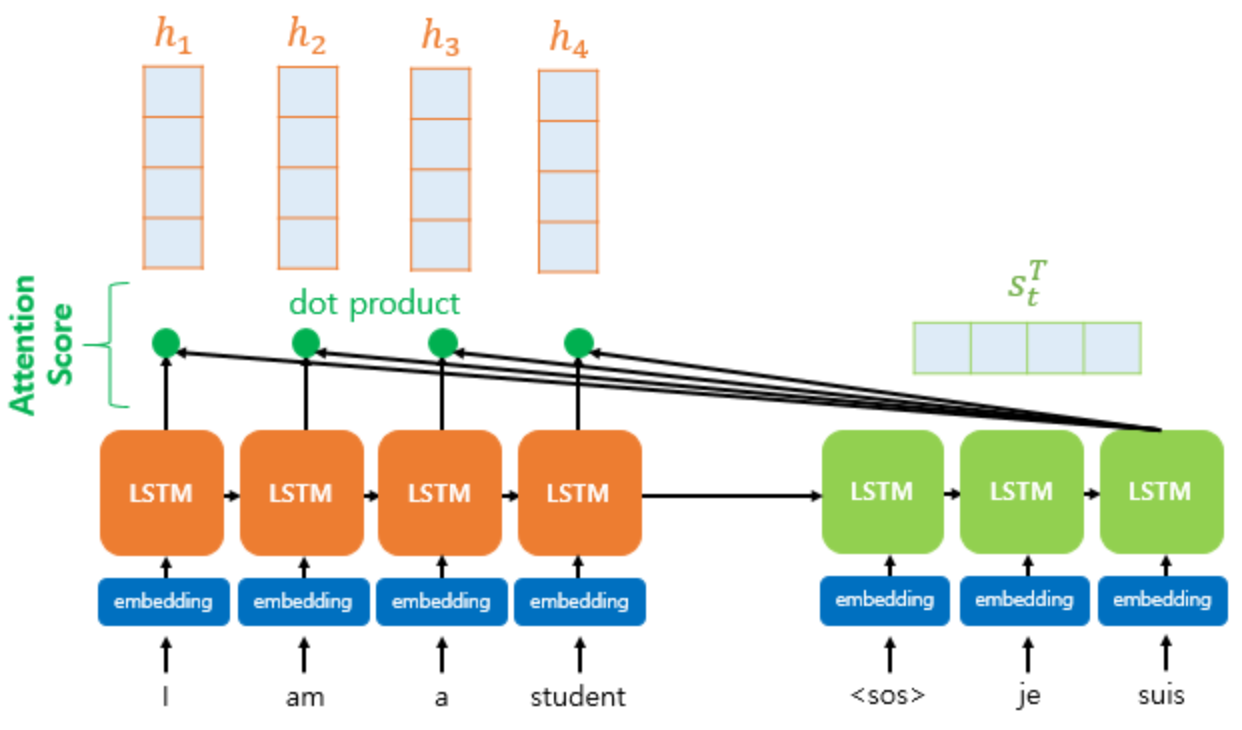
하지만 $score(s_{t}, h_{i}) = s_{t}^{T}h_{i}$
- $s_t$ : t 시점 decoder 셀의 hidden state
- $h_i$ : i 시점 encoder 셀의 hidden state
score 계산을 위해 encoder 셀의 모든 hidden state들과, decoder에서 t 시점에 해당하는 hidden state인 Query를 전치시켜서 곱한다.
Attention score의 모음값 = $e^t = [s_{t}^{T}h_{1}, ..., s_{t}^{T}h_{N}]$
Step2. Attention Distribution구하기
Attention score 모음값들을 softmax에 통과시켜
Attention Distribution $\alpha^{t}$ = softmax( $e^{t}$ ) 를 얻는다.
해당 분포를 통해서 어떤 시점에서의 hidden state가 얼마나 영향을 미치는 지 파악할 수 있다.
- softmax를 활용한 이유는 전체 합이 1이 된다는 점, 그리고 전체 합(분모) 중 얼마나 비중을 차지하는 지를 표현하기 떄문이다.
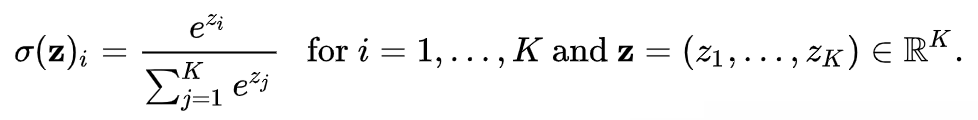
Step3. Attention Value 구하기
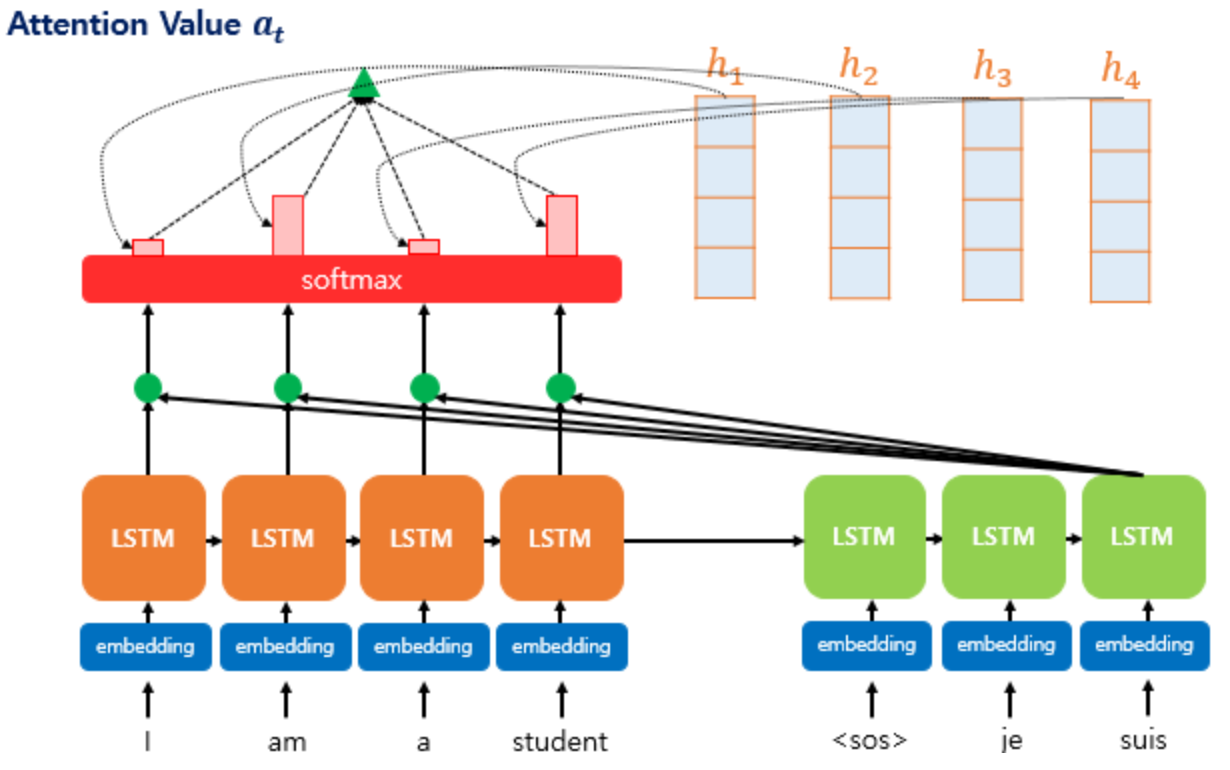
Attention score를 통해서 정해진 비율과 Encoder state의 각 시점에서의 hidden state를 곱해
Attention Value(context vector) = $a_t = \sum_{i=1}^{N} \alpha_i^th_i$ 를 구합니다.
Attention is all you need에서 제공한 수식을 Scaled Dot-Product Attention 수식을 보면 Step1~3이 한번에 압축된 수식으로 소개된다.
Attention$(Q,K,V)$ = softmax$(\frac{QK^T}{\sqrt{d_k}})V$ 으로 표현되어있다.
- $Q$ : Query, t 시점에 해당하는 decoder 셀의 hidden state(유추하기 위한 정보)
- $K$ : Key, 모든 시점에 해당하는 encoder 셀의 hidden states(검토하기 위한 정보)
- $V$ : Value, 모든 시점에 해당하는 encoder 셀에서의 hidden states(비율을 적용하기 위한 정보)
- $d_k$ : Query와 Key의 차원
즉, Step2의 Attention score를 구하는 수식에 크기만큼 나누어 사용(Scaling)하는 차이가 존재한다.
Step4. Attention Value과 Decoder의 t시점 연결
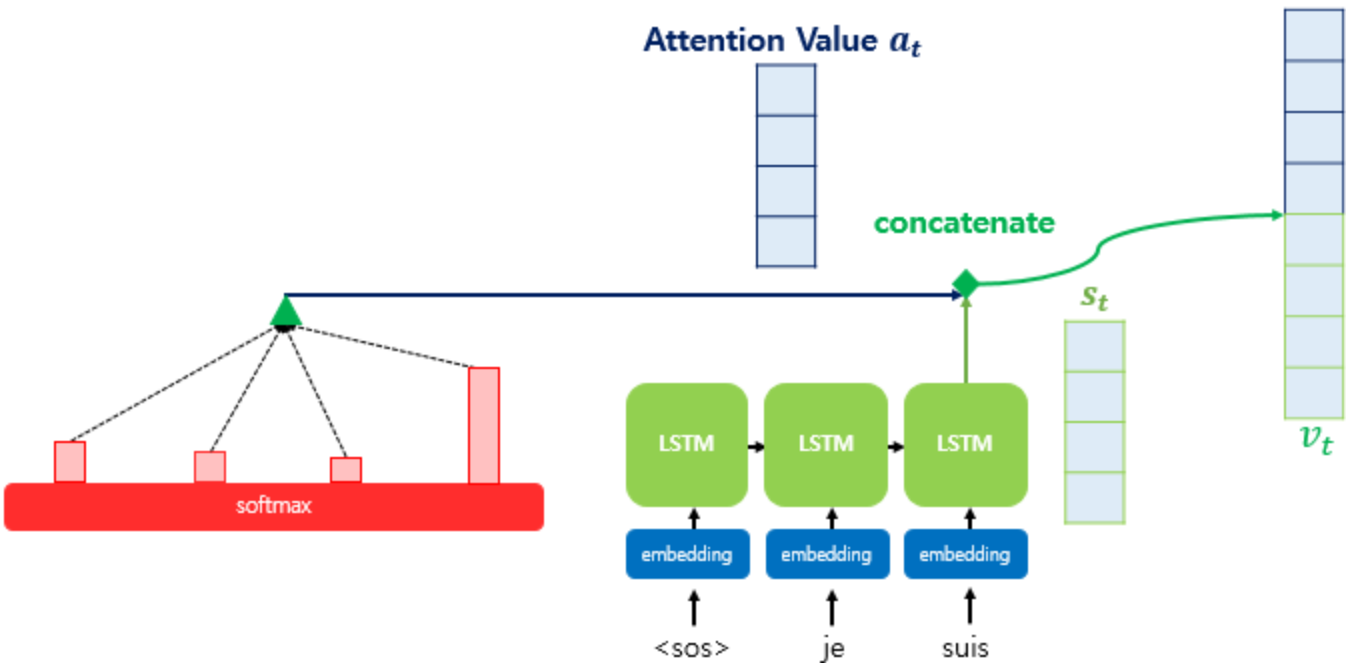
Attention Value와 Decoder의 t시점 hidden state를 concatenate하여 하나의 벡터를 만들고 이를 통해 예측을 진행한다.
'인공지능 > 기초' 카테고리의 다른 글
| LSTM & GRU (0) | 2024.05.07 |
|---|---|
| Sequence-to-sequence(seq2seq) & Teacher-forcing (0) | 2024.04.27 |
| Applications of RNNs (0) | 2024.03.23 |
| Recurrent Neural Network (2) | 2024.03.23 |