LSTM (Long Short Term Memory)
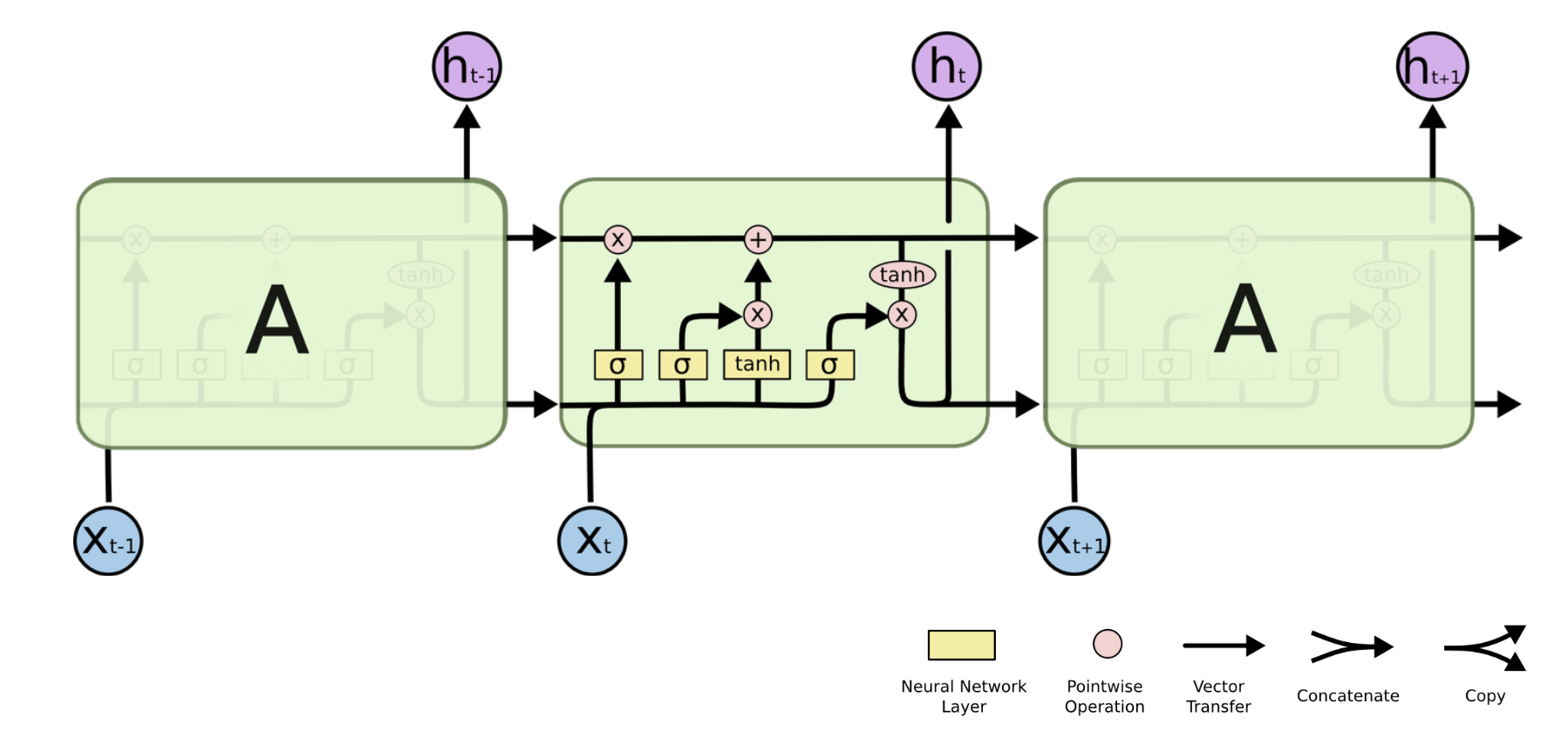
LSTM은 Hochreiter & Schmidhuber (1997) 에서 처음 소개되었다. RNN에서 발생할 수 있는 Vanishing Gradient Problem을 해결하기 위해 Cell gate를 활용한다. 이는 장기기억 즉, 과거의 먼 시점의 input을 기억할 수 있도록 한다.
RNN은 총 2개의 input, hidden state $h_{t-1}$ 과 현재 시점의 input $X_t$ 를 활용하지만
LSTM은 이전 시점에서 오는 hidden state $h_{t-1}$ , Cell state $C_{t-1}$ 그리고 현재 시점의 input $X_t$ 총 3개를 Input으로 활용한다.
LSTM의 단게별 설명
 |
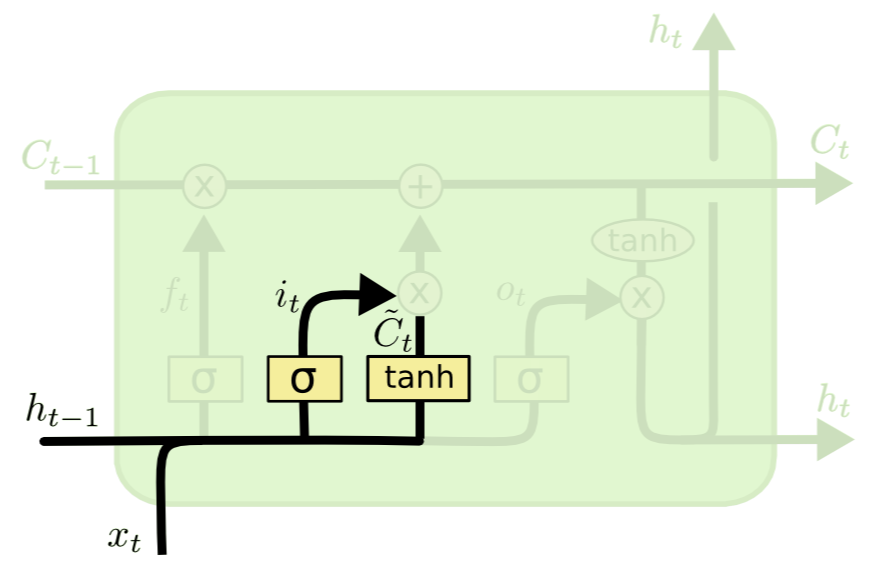 |
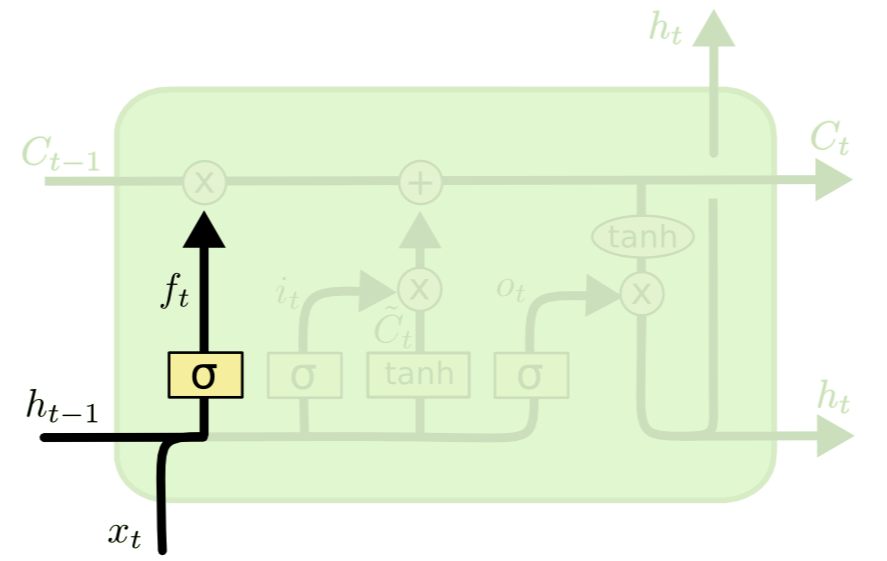
| Forget gate layer | Input gate layer |
| sigmoid $\sigma$ 를 활용하여 hidden state $h_{t-1}$ 과 Input $x_t$ 의 비율을 0~1 사이로 조정한다. 0은 모두 잊어버리게(forget) 1은 모두 활용하도록한다. | 현재의 Cell state 값에 얼마나 저장할 지를 정한다. sigmoid $\sigma$ 는 어떤 값이 얼마나 업데이트 될 지 정한다. tanh 는 $\widetilde{C_t}$ state에 더해질 수 있는 새로운 후보 값을 만들어낸다. |
| $f_t = \sigma (W_f \cdot [h_{t-1}, x_t]+b_f)$ | $i_t = \sigma(W_i \cdot[h_{t-1}, x_t] + b_i)$ $\widetilde{C}_t = tanh(W_C \cdot[h_{t-1}, x_t] + b_C)$ |
 |
 |
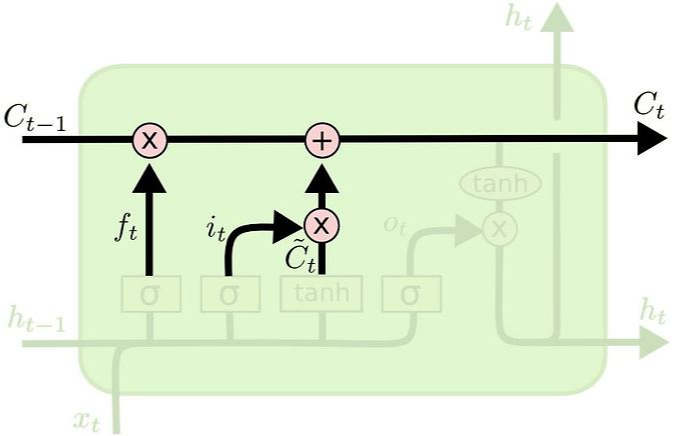
| Update | Output gate |
| LSTM의 존재 이유. 앞에서 언급했듯이 더 이전의 state 정보를 유지할 수 있게 한다. Linear Interaction만을 적용시킨 것이 특징이다. 해당 과정에서는 과거의 Cell state를 업데이트 한다. Forget gate에서 얼마나 버릴 지, Input gate에서 얼마나 더할 지 정해졌기 때문에 update 과정에서 계산을 통해 이를 Cell state 업데이트 한다. |
어떤 출력값을 출력할 지 정하는 과정. Cell state를 기반으로 정해지며, Cell state를 tanh 를 통과시켜 -1 ~ 1 사이의 값을 가지게 하고, sigmoid를 통과한 값과 곱한다. $h_t$ 는 다음 시점와 output으로 출력되게 된다. |
| $C_t = f_t \ast C_{t-1} + i_t \ast \widetilde{C}_t$ | $o_t = \sigma (W_o \cdot [h_{t-1}, x_t] + b_o)$ $h_t = o_t \ast tanh(C_t)$ |
반응형
GRU(Gated Recurrent Unit)
이런 LSTM을 개량해서 Cho, et al. (2014) 에서 GRU(Gated Recurrent Unit)를 발표하였다. forget gate와 input gate를 통합하여 update gate를 만들어 내었다.
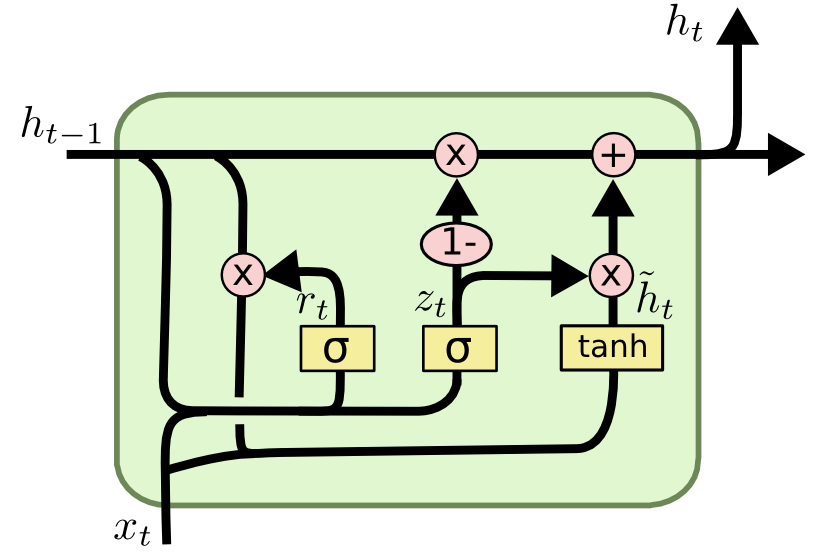 |
$z_t = \sigma (W_z \cdot [h_{t-1}, x_t])$ $r_t = \sigma (W_r \cdot [h_{t-1}, x_t])$ $\widetilde{h}_t = tanh(W \cdot [r_t \ast h_{t-1}, x_t])$ $h_t = (1-z_t) \ast h_{t-1} + z_t \ast \widetilde{h}_t$ |
반응형
'인공지능 > 기초' 카테고리의 다른 글
| (Scaled) Dot-Product Attention (0) | 2024.04.28 |
|---|---|
| Sequence-to-sequence(seq2seq) & Teacher-forcing (0) | 2024.04.27 |
| Applications of RNNs (0) | 2024.03.23 |
| Recurrent Neural Network (2) | 2024.03.23 |